Stacks are dynamic data structures that follow the Last In First Out (LIFO) principle. The last item to be inserted into a stack is the first one to be deleted from it.

For example, let’s say you have a stack of trays on a table. The tray at the top of the stack is the first item to be moved if you require a tray from that stack.

Inserting and deleting elements

Stacks have restrictions on the insertion and deletion of elements. Elements can be inserted or deleted only from one end of the stack i.e. from the top. The element at the top is called the top element. The operations of inserting and deleting elements are called push() and pop() respectively.

When the top element of a stack is deleted, if the stack remains non-empty, then the element just below the previous top element becomes the new top element of the stack.

For example, in the stack of trays, if you take the tray on the top and do not replace it, then the second tray automatically becomes the top element (tray) of that stack.

Features of stacks

• Dynamic data structures
• Does not have a fixed size
• Does not consume a fixed amount of memory
• Size of stack changes with each push() and pop() operation. Each push() and pop() operation increases and decreases the size of the stack by 1, respectively.

A stack can be visualized as follows:

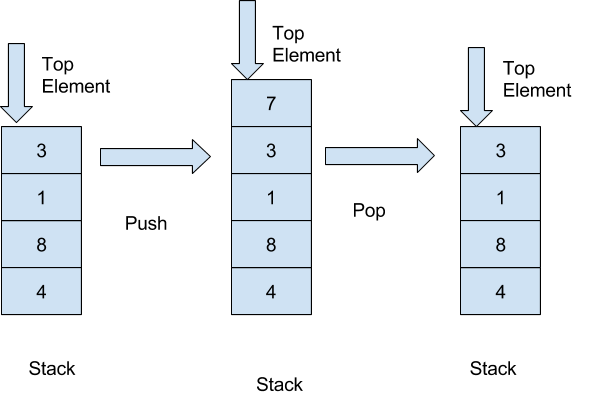
Now, let us write some code snippets to perform the push and pop operations. The code is in C++ but it is pretty easy to understand.

Push

void push (int stack[ ] , int x , int n) {
if ( top == n-1 ) {         //If the top position is the last of position in a stack, this means that the stack is full
   cout << “Stack is full.Overflow condition!” ;
   }
   else{
       top = top +1 ;            //Incrementing top position 
       stack[ top ] = x ;       //Inserting element on incremented position  
   }
}

Pop

Removes an element from the top of a stack.

void pop (int stack[ ] ,int n ) {
   if( isEmpty () ) {
     cout << “Stack is empty. Underflow condition! ” << endl ;
   } else {
     top = top - 1 ; //Decrementing top’s position will detach last element from stack            
   }
}

Top Element

Access the top element of a stack.

int topElement ( ) {
   return stack[ top ];
}

Size

Determines the current size of a stack.

int size ( ) {
   return top + 1;
}

Implementation

Determines the current size of a stack.

#include <iostream>
using namespace std;
int top = -1; //Globally defining the value of top as the stack is empty

void push (int stack[ ] , int x , int n)
{
    if ( top == n-1 )    //If the top position is the last of position of the stack, this means that the stack is full.
    {
        cout << "Stack is full.Overflow condition!" ;
    }
    else
    {
        top = top +1 ;         //Incrementing the top position
        stack[ top ] = x ;    //Inserting an element on incremented position 
    }
}
bool isEmpty ( )
{
    if ( top == -1 )  //Stack is empty
        return true ;
    else
       return false;
}
void pop ( )
{

    if( isEmpty ( ) )
    {
        cout << "Stack is empty. Underflow condition! " << endl ;
    }
    else 
    {
         top = top - 1 ; //Decrementing top’s position will detach last element from stack           
    }
}
int size ( )
{
    return top + 1;
}
int topElement (int stack[])
{
    return stack[ top ];
}
//Let's implement these functions on the stack given above

int main( )
{
    int stack[ 3 ];
    // pushing element 5 in the stack .
    push(stack , 5 , 3 ) ;

    cout << "Current size of stack is " << size ( ) << endl ;

    push(stack , 10 , 3);
   push (stack , 24 , 3) ;

    cout << "Current size of stack is " << size( ) << endl ;

    //As the stack is full, further pushing will show an overflow condition.
    push(stack , 12 , 3) ;

    //Accessing the top element
    cout << "The current top element in stack is " << topElement(stack) << endl;

    //Removing all the elements from the stack
    for(int i = 0 ; i < 3;i++ )
        pop( );
    cout << "Current size of stack is " << size( ) << endl ;

    //As the stack is empty , further popping will show an underflow condition.
    pop ( ); 

}

Output

• Current size of stack: 1
• Current size of stack: 3
• Current top element in stack: 24 (Stack is full. Overflow condition!)
• Current size of stack: 0 (Stack is empty. Underflow condition!)

Example

Now, to understand the concept practically, let us consider an example of a balanced parentheses problem.

You have a bracket sequence made up of opening '(' and closing ')' parentheses. You must check if this bracket sequence is balanced.

A bracket sequence is considered balanced if for every prefix of the sequence, the number of opening brackets is greater than or equal to the number of closing brackets, and the total number of opening brackets is equal to the number of closing brackets.

You can check this using a stack. Let's see how.

You can maintain a stack where you store a parenthesis. Whenever, you come across an opening parenthesis, push it in the stack. However, whenever you come across a closing parenthesis, pop a parenthesis from the stack.

#include <iostream>
using namespace std;
int top;
void  check (char str[ ], int n, char stack [ ])
{
    for(int i = 0 ; i < n ; i++ )
    {
        if (str [ i ] == ‘(’)
        {
            top = top + 1;
            stack[ top ] = ‘ ( ’;
        }
        if(str[ i ] == ‘)’ )
        {
            if(top == -1 )
            {
                top = top -1 ;
                break ;
             }
            else
            {
                 top = top -1 ;
            }
        }
    }
    if(top == -1)
        cout << “String is balanced!” << endl;
    else
        cout << “String is unbalanced!” << endl ;
}

int main ( )
   {
    //balanced parenthesis string.
    char str[  ] = { ‘(‘ , ‘a’ , ‘+’, ‘ ( ’, ‘b ’ , ‘-’ , ‘ c’ ,‘)’ , ‘ ) ’} ;

    // unbalanced string .
       char str1 [ ] = { ‘(’ , ‘(’ , ‘a’ , ‘ + ’ , ‘ b’ , ‘)’ } ;
    char stack [ 15 ] ;
    top = -1;  
       check (str , 9 , stack );   //Passing balanced string  
       top = -1 ;
    check(str1 , 5 , stack) ; //Passing unbalanced string
    return 0;

}

Output

String is balanced! 
String is unbalanced!

Analysis of Stacks

Listed below are the time complexities for various operations that can be performed on the Stack data structure.

• Push Operation : O(1)
• Pop Operation : O(1)
• Top Operation : O(1)
• Search Operation : O(n)

Applications of Stack

The simplest application of a stack is to reverse a word. You push a given word to stack—letter by letter—and then pop letters from the stack.

There are other uses also such as: Parsing, Expression Conversion (Infix to Postfix, Postfix to Prefix etc) and many more.

Any modern computer environment uses a stack as the primary memory management model for a running program.  Whether it's native code (x86, Sun, VAX) or JVM, a stack is at the center of the run-time environment for Java, C++, Ada, FORTRAN, etc.